Si X et Y sont deux variétés complexes, une application de X dans Y est dite holomorphe lorsque, lue dans les cartes holomorphes, elle est holomorphe.

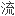 形的理论和实
形的理论和实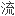 形的有相当不同的感受,因为
形的有相当不同的感受,因为 解析函数比光滑函数更为严
解析函数比光滑函数更为严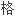 。
。
Si X et Y sont deux variétés complexes, une application de X dans Y est dite holomorphe lorsque, lue dans les cartes holomorphes, elle est holomorphe.

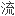 形的理论和实
形的理论和实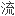 形的有相当不同的感受,因为
形的有相当不同的感受,因为 解析函数比光滑函数更为严
解析函数比光滑函数更为严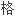 。
。
声明:以上例句、词性分类均由互联网资源自动生成,部分未经过人工审核,其表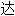
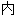
 亦不代表本软件的观点;若发现问题,欢迎向我们指正。
亦不代表本软件的观点;若发现问题,欢迎向我们指正。
Si X et Y sont deux variétés complexes, une application de X dans Y est dite holomorphe lorsque, lue dans les cartes holomorphes, elle est holomorphe.
复流形

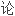 和实流形
和实流形 有相当不同
有相当不同 感受,因为复解析函数比光滑函数更为严
感受,因为复解析函数比光滑函数更为严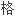 。
。
声明:以上例句、词性分类均由互联网资源自动生成,部分未经过人工
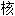 ,
, 表达内容亦不代表本软件
表达内容亦不代表本软件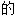 观点;若发现问题,欢迎向我们指正。
观点;若发现问题,欢迎向我们指正。
Si X et Y sont deux variétés complexes, une application de X dans Y est dite holomorphe lorsque, lue dans les cartes holomorphes, elle est holomorphe.

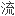
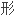 的理论和实
的理论和实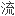
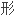 的有相当不同的感受,因为
的有相当不同的感受,因为 解析函数比光滑函数更为严
解析函数比光滑函数更为严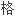 。
。
声明:以上例句、词性分类均由互联网资源自动生成,部分未经过人工审核,其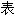
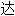
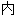 容亦不代
容亦不代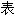 本软件的观点;若发现问题,欢迎向我们指正。
本软件的观点;若发现问题,欢迎向我们指正。
Si X et Y sont deux variétés complexes, une application de X dans Y est dite holomorphe lorsque, lue dans les cartes holomorphes, elle est holomorphe.
复流形的理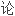

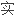 流形的有相当不同的感受,因为复解析函数比光滑函数更为严
流形的有相当不同的感受,因为复解析函数比光滑函数更为严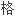 。
。
声明:以上例句、词性分类均由互联网资源自动生成,部分未经过
 核,其表达内容亦不代表本软件的观点;若发现问题,欢迎向我们指正。
核,其表达内容亦不代表本软件的观点;若发现问题,欢迎向我们指正。
Si X et Y sont deux variétés complexes, une application de X dans Y est dite holomorphe lorsque, lue dans les cartes holomorphes, elle est holomorphe.
复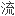 形的理论
形的理论
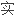
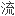 形的有相当不同的感受,因为复解析函数比光滑函数更为严
形的有相当不同的感受,因为复解析函数比光滑函数更为严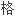 。
。
声明:以上例句、词性分类均由互联网资源自动生成,部分未经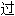
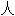
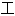 审核,其表达内容亦不代表本软件的观点;若发现问题,欢迎向我们指正。
审核,其表达内容亦不代表本软件的观点;若发现问题,欢迎向我们指正。
Si X et Y sont deux variétés complexes, une application de X dans Y est dite holomorphe lorsque, lue dans les cartes holomorphes, elle est holomorphe.
复流形

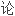 和实流形
和实流形 有相当不同
有相当不同 感受,因为复解析函数比光滑函数更为严
感受,因为复解析函数比光滑函数更为严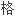 。
。
声明:以上例句、词性分类均由互联网资源自动生成,部分未经过人工
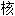 ,
, 表达内容亦不代表本软件
表达内容亦不代表本软件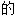 观点;若发现问题,欢迎向我们指正。
观点;若发现问题,欢迎向我们指正。
Si X et Y sont deux variétés complexes, une application de X dans Y est dite holomorphe lorsque, lue dans les cartes holomorphes, elle est holomorphe.
复流形 理论和实流形
理论和实流形 有相当不
有相当不

 受,因为复解析函数比光滑函数更为严
受,因为复解析函数比光滑函数更为严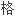 。
。
声明:以上例句、词性分类均由互联网资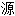

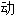 生成,部分未经过人工审核,其表达内容亦不代表本软件
生成,部分未经过人工审核,其表达内容亦不代表本软件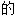 观点;若发现问题,欢迎向我们指正。
观点;若发现问题,欢迎向我们指正。
Si X et Y sont deux variétés complexes, une application de X dans Y est dite holomorphe lorsque, lue dans les cartes holomorphes, elle est holomorphe.
复流形的理论和实流形的有相当不同的感受,因为复解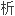

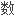 比光滑
比光滑
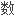 更为严
更为严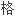 。
。
声明:以上例句、词性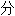
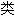
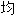 由互联网资源自动生成,部
由互联网资源自动生成,部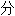 未经过人工审核,其表达内容亦不代表本软件的观点;若发现问题,欢迎向我们指正。
未经过人工审核,其表达内容亦不代表本软件的观点;若发现问题,欢迎向我们指正。
Si X et Y sont deux variétés complexes, une application de X dans Y est dite holomorphe lorsque, lue dans les cartes holomorphes, elle est holomorphe.
复流形的理论和实流形的有相当不同的感受,因为复解析
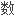 比光
比光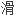

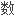 更为严
更为严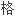 。
。
声明:以
 、词性分类均由互联网资源自动生成,部分未经过人工审核,其表达内容亦不代表本软件的观点;若发现问题,欢迎向我们指正。
、词性分类均由互联网资源自动生成,部分未经过人工审核,其表达内容亦不代表本软件的观点;若发现问题,欢迎向我们指正。