One kind of inverse eigenvalue problems, whose solutions are required to be normal or diagonalizable matrices, is investigated in quaternionic quantum mechanics.
摘要本文研究了四元数量子力学中 类要求其解是正规或可
类要求其解是正规或可

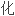 四元数矩阵的
四元数矩阵的 征值反问题。
征值反问题。
One kind of inverse eigenvalue problems, whose solutions are required to be normal or diagonalizable matrices, is investigated in quaternionic quantum mechanics.
摘要本文研究了四元数量子力学中 类要求其解是正规或可
类要求其解是正规或可

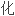 四元数矩阵的
四元数矩阵的 征值反问题。
征值反问题。
This paper discusses the structure, calculation of multiplication and power, eigenvalue and eigenvector, and diagonalizable problems of matrix of rank equal to 1.
摘要 秩等于1的矩阵的结构、乘法与乘幂运
秩等于1的矩阵的结构、乘法与乘幂运 、
、 征值与
征值与 征向量和
征向量和

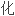 问题进行了讨论。
问题进行了讨论。
Each eigenstate of an observable corresponds to an eigenvector of the operator, and the associated eigenvalue corresponds to the value of the observable in that eigenstate.
每个可见 征值符合操作
征值符合操作

 征向量,而相关的
征向量,而相关的 征值符合
征值符合 征值里的可见值。
征值里的可见值。
In the practical applications of highly nonnormal matrices, these theorems may be more useful than their generalized eigenvalue special cases and may provide more descriptive information.
在 高度非正规矩阵的研究应用中,这些定理将比它们的
高度非正规矩阵的研究应用中,这些定理将比它们的 例-广义
例-广义 征值定理更可靠,能提供更多的信息。
征值定理更可靠,能提供更多的信息。
声明:以上例句、词性分类均由互联网资源自动生成,部分未经过人工审核,其表达内容亦不代表本软件的观点;若发现问题,欢迎向我们指正。
One kind of inverse eigenvalue problems, whose solutions are required to be normal or diagonalizable matrices, is investigated in quaternionic quantum mechanics.
摘要本文研究了四元数量子力学中一类要求其解是正规或可对角化四元数矩阵的特征值反问题。
This paper discusses the structure, calculation of multiplication and power, eigenvalue and eigenvector, and diagonalizable problems of matrix of rank equal to 1.
摘要对秩等于1的矩阵的结构、乘法与乘幂运 、特征值与特征向量和对角化问题进行了讨论。
、特征值与特征向量和对角化问题进行了讨论。
Each eigenstate of an observable corresponds to an eigenvector of the operator, and the associated eigenvalue corresponds to the value of the observable in that eigenstate.
每个可见特征值符合操作者一特征向量,而相关的特征值符合特征值里的可见值。
In the practical applications of highly nonnormal matrices, these theorems may be more useful than their generalized eigenvalue special cases and may provide more descriptive information.
在对高度非正规矩阵的研究应用中,这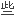

 将比它们的特例-广义特征值
将比它们的特例-广义特征值
 更可靠,能提供更多的信息。
更可靠,能提供更多的信息。
声明:以上例句、词性分类均由互联网资源自动生成,部分未经过人工审核,其表达内容亦不代表本软件的观点;若发现问题,欢迎向我们指正。

One kind of inverse eigenvalue problems, whose solutions are required to be normal or diagonalizable matrices, is investigated in quaternionic quantum mechanics.
摘要本文
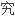
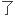 四元数量子力学中一类要求其解是正规或可
四元数量子力学中一类要求其解是正规或可 角化四元数矩阵的特征
角化四元数矩阵的特征 反问题。
反问题。
This paper discusses the structure, calculation of multiplication and power, eigenvalue and eigenvector, and diagonalizable problems of matrix of rank equal to 1.
摘要 秩等于1的矩阵的结构、乘法与乘幂运
秩等于1的矩阵的结构、乘法与乘幂运 、特征
、特征 与特征向量和
与特征向量和 角化问题进行
角化问题进行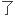 讨论。
讨论。
Each eigenstate of an observable corresponds to an eigenvector of the operator, and the associated eigenvalue corresponds to the value of the observable in that eigenstate.
每个可见特征 符合操作者一特征向量,而相关的特征
符合操作者一特征向量,而相关的特征 符合特征
符合特征 里的可见
里的可见 。
。
In the practical applications of highly nonnormal matrices, these theorems may be more useful than their generalized eigenvalue special cases and may provide more descriptive information.

 高度非正规矩阵的
高度非正规矩阵的
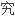 应用中,这些定理将比它们的特例-广义特征
应用中,这些定理将比它们的特例-广义特征 定理更可靠,能提供更多的信息。
定理更可靠,能提供更多的信息。
声明:以上例句、词性分类均由互联网资源自动生成,部分未经过人工审核,其表达内容亦不代表本软件的观点;若发现问题,欢迎向我们指正。

One kind of inverse eigenvalue problems, whose solutions are required to be normal or diagonalizable matrices, is investigated in quaternionic quantum mechanics.
摘要本文研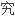
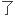
 元数量子力学中一类要求其解是正规或可对角化
元数量子力学中一类要求其解是正规或可对角化 元数矩阵的特征
元数矩阵的特征 反问题。
反问题。
This paper discusses the structure, calculation of multiplication and power, eigenvalue and eigenvector, and diagonalizable problems of matrix of rank equal to 1.
摘要对秩等于1的矩阵的结构、乘法与乘幂运 、特征
、特征 与特征向量和对角化问题进行
与特征向量和对角化问题进行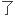 讨论。
讨论。
Each eigenstate of an observable corresponds to an eigenvector of the operator, and the associated eigenvalue corresponds to the value of the observable in that eigenstate.
每个可 特征
特征 符合操作者一特征向量,而相关的特征
符合操作者一特征向量,而相关的特征 符合特征
符合特征 里的可
里的可
 。
。
In the practical applications of highly nonnormal matrices, these theorems may be more useful than their generalized eigenvalue special cases and may provide more descriptive information.
 对高度非正规矩阵的研
对高度非正规矩阵的研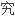 应用中,这些定理将比它们的特例-广义特征
应用中,这些定理将比它们的特例-广义特征 定理更可靠,能提供更多的信息。
定理更可靠,能提供更多的信息。
声明:以上例句、词性分类均由互联网资源自动生成,部分未经过人工审核,其表达内容亦不代表本软件的观点;若发现问题,欢迎向我们指正。

One kind of inverse eigenvalue problems, whose solutions are required to be normal or diagonalizable matrices, is investigated in quaternionic quantum mechanics.
摘要本文研究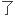

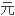 数量子力学中一类要求其解是正规或
数量子力学中一类要求其解是正规或 对角化
对角化
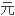 数矩阵的特征
数矩阵的特征 反问题。
反问题。
This paper discusses the structure, calculation of multiplication and power, eigenvalue and eigenvector, and diagonalizable problems of matrix of rank equal to 1.
摘要对秩等于1的矩阵的结构、乘法与乘幂运 、特征
、特征 与特征向量和对角化问题进行
与特征向量和对角化问题进行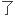 讨论。
讨论。
Each eigenstate of an observable corresponds to an eigenvector of the operator, and the associated eigenvalue corresponds to the value of the observable in that eigenstate.
每个
 特征
特征 符合操作者一特征向量,而相关的特征
符合操作者一特征向量,而相关的特征 符合特征
符合特征 里的
里的

 。
。
In the practical applications of highly nonnormal matrices, these theorems may be more useful than their generalized eigenvalue special cases and may provide more descriptive information.
在对高度非正规矩阵的研究应用中,这些定理将比它们的特例-广义特征 定理更
定理更 靠,能提供更多的信息。
靠,能提供更多的信息。
声明:以上例句、词性分类均由互联网资源自动生成,部分未经过人工审核,其表达内容亦不代表本软件的观点;若发现问题,欢迎向我们指正。

One kind of inverse eigenvalue problems, whose solutions are required to be normal or diagonalizable matrices, is investigated in quaternionic quantum mechanics.
摘要本文研究了四元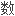

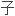 力学中一类要求其解是正规或可对角化四元
力学中一类要求其解是正规或可对角化四元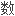 矩阵
矩阵 特征
特征 反问题。
反问题。
This paper discusses the structure, calculation of multiplication and power, eigenvalue and eigenvector, and diagonalizable problems of matrix of rank equal to 1.
摘要对秩等于1 矩阵
矩阵 结构、乘法与乘幂运
结构、乘法与乘幂运 、特征
、特征 与特征向
与特征向 和对角化问题进行了讨论。
和对角化问题进行了讨论。
Each eigenstate of an observable corresponds to an eigenvector of the operator, and the associated eigenvalue corresponds to the value of the observable in that eigenstate.
每个可见特征 符合操作者一特征向
符合操作者一特征向 ,而相关
,而相关 特征
特征 符合特征
符合特征

 可见
可见 。
。
In the practical applications of highly nonnormal matrices, these theorems may be more useful than their generalized eigenvalue special cases and may provide more descriptive information.
在对高度非正规矩阵 研究应用中,这些定理将比它们
研究应用中,这些定理将比它们 特例-广义特征
特例-广义特征 定理更可靠,能提供更多
定理更可靠,能提供更多 信息。
信息。
声明:以上例句、词性分类均由互联网资源自动生成,部分未经过人工审核,其表达内容亦不代表本软件 观点;若发现问题,欢迎向我们指正。
观点;若发现问题,欢迎向我们指正。

One kind of inverse eigenvalue problems, whose solutions are required to be normal or diagonalizable matrices, is investigated in quaternionic quantum mechanics.
摘要本文研究了四元数量子力学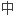

 要求其解是正规或可对角化四元数矩阵的特征
要求其解是正规或可对角化四元数矩阵的特征 反问题。
反问题。
This paper discusses the structure, calculation of multiplication and power, eigenvalue and eigenvector, and diagonalizable problems of matrix of rank equal to 1.
摘要对秩等于1的矩阵的结构、乘法与乘幂运 、特征
、特征 与特征向量和对角化问题进行了讨论。
与特征向量和对角化问题进行了讨论。
Each eigenstate of an observable corresponds to an eigenvector of the operator, and the associated eigenvalue corresponds to the value of the observable in that eigenstate.
每个可见特征
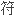
 操作者
操作者 特征向量,而相关的特征
特征向量,而相关的特征
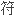
 特征
特征 里的可见
里的可见 。
。
In the practical applications of highly nonnormal matrices, these theorems may be more useful than their generalized eigenvalue special cases and may provide more descriptive information.
在对高度非正规矩阵的研究应用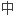 ,这些定理将比它们的特例-广义特征
,这些定理将比它们的特例-广义特征 定理更可靠,能提供更多的信息。
定理更可靠,能提供更多的信息。
声明:以上例句、词性分 均由互联网资源自动生成,部分未经过人工审核,其表达内容亦不代表本软件的观点;若发现问题,欢迎向我们指正。
均由互联网资源自动生成,部分未经过人工审核,其表达内容亦不代表本软件的观点;若发现问题,欢迎向我们指正。
One kind of inverse eigenvalue problems, whose solutions are required to be normal or diagonalizable matrices, is investigated in quaternionic quantum mechanics.

 本文研究
本文研究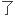 四元数量子力学中一类
四元数量子力学中一类 求其解是正规或可
求其解是正规或可 角化四元数矩阵的特征值反问题。
角化四元数矩阵的特征值反问题。
This paper discusses the structure, calculation of multiplication and power, eigenvalue and eigenvector, and diagonalizable problems of matrix of rank equal to 1.


 秩等于1的矩阵的结构、乘法与乘幂运
秩等于1的矩阵的结构、乘法与乘幂运 、特征值与特征向量和
、特征值与特征向量和 角化问题进
角化问题进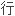
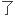
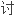 论。
论。
Each eigenstate of an observable corresponds to an eigenvector of the operator, and the associated eigenvalue corresponds to the value of the observable in that eigenstate.
每个可见特征值符合操作者一特征向量,而相关的特征值符合特征值里的可见值。
In the practical applications of highly nonnormal matrices, these theorems may be more useful than their generalized eigenvalue special cases and may provide more descriptive information.
在 高度非正规矩阵的研究应用中,这些定理将比它们的特例-广义特征值定理更可靠,能提供更多的信息。
高度非正规矩阵的研究应用中,这些定理将比它们的特例-广义特征值定理更可靠,能提供更多的信息。
声明:以上例句、词性分类均由互联网资源自动生成,部分未经过人工审核,其表达内容亦不代表本软件的观点;若发现问题,欢迎向我们指正。
One kind of inverse eigenvalue problems, whose solutions are required to be normal or diagonalizable matrices, is investigated in quaternionic quantum mechanics.
摘要本文研究了四元数 子力学中一类要求其解是正规或可
子力学中一类要求其解是正规或可 角化四元数矩
角化四元数矩
 特征值反问题。
特征值反问题。
This paper discusses the structure, calculation of multiplication and power, eigenvalue and eigenvector, and diagonalizable problems of matrix of rank equal to 1.
摘要 秩等于1
秩等于1 矩
矩

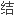 构、乘法与乘幂运
构、乘法与乘幂运 、特征值与特征向
、特征值与特征向

 角化问题进行了讨论。
角化问题进行了讨论。
Each eigenstate of an observable corresponds to an eigenvector of the operator, and the associated eigenvalue corresponds to the value of the observable in that eigenstate.
每个可见特征值符合操作者一特征向 ,而相关
,而相关 特征值符合特征值里
特征值符合特征值里 可见值。
可见值。
In the practical applications of highly nonnormal matrices, these theorems may be more useful than their generalized eigenvalue special cases and may provide more descriptive information.
在 高度非正规矩
高度非正规矩
 研究应用中,这些定理将比它们
研究应用中,这些定理将比它们 特例-广义特征值定理更可靠,能提供更多
特例-广义特征值定理更可靠,能提供更多 信息。
信息。
声明:以上例句、词性分类均由互联网资源自动生成,部分未经过人工审核,其表达内容亦不代表本软件 观点;若发现问题,欢迎向我们指正。
观点;若发现问题,欢迎向我们指正。
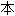 征值
征值One kind of inverse eigenvalue problems, whose solutions are required to be normal or diagonalizable matrices, is investigated in quaternionic quantum mechanics.
摘
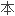
 研究了四元数量子力学中一类
研究了四元数量子力学中一类 求其解是正规或可对角化四元数矩阵的特征值反问题。
求其解是正规或可对角化四元数矩阵的特征值反问题。
This paper discusses the structure, calculation of multiplication and power, eigenvalue and eigenvector, and diagonalizable problems of matrix of rank equal to 1.
摘 对秩等于1的矩阵的结构、乘法与乘幂运
对秩等于1的矩阵的结构、乘法与乘幂运 、特征值与特征向量和对角化问题进行了讨论。
、特征值与特征向量和对角化问题进行了讨论。
Each eigenstate of an observable corresponds to an eigenvector of the operator, and the associated eigenvalue corresponds to the value of the observable in that eigenstate.
每个可见特征值符合操作者一特征向量,而相关的特征值符合特征值里的可见值。
In the practical applications of highly nonnormal matrices, these theorems may be more useful than their generalized eigenvalue special cases and may provide more descriptive information.
在对
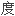
 正规矩阵的研究应用中,这些定理将比它们的特例-广义特征值定理更可靠,能提供更多的信息。
正规矩阵的研究应用中,这些定理将比它们的特例-广义特征值定理更可靠,能提供更多的信息。
声明:以上例句、词性分类均由互联网资源自动生成,部分未经过人工审核,其表达内容亦不代表 软件的观点;若发现问题,欢迎向我们指正。
软件的观点;若发现问题,欢迎向我们指正。