All graphs are finite simple undirected graph with no isolated vertices in this paper. It is completed the classification of graphs on which a semidihedral group acts edge-transitively.
运用图的自同构理论,获得了关于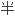
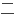
 体群边传递的图Γ的完全分类。
体群边传递的图Γ的完全分类。
All graphs are finite simple undirected graph with no isolated vertices in this paper. It is completed the classification of graphs on which a semidihedral group acts edge-transitively.
运用图的自同构理论,获得了关于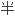
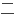
 体群边传递的图Γ的完全分类。
体群边传递的图Γ的完全分类。
These observations allow one to formalize the definition of reflection: a reflection is an involutive isometry of an Euclidean space whose set of fixed points is an affine subspace of codimension 1.
这些观察允许我们形式化反射的定义: 反射是欧几里得空间的对合等距同构,它的不动点集合是余维度为 1 的仿射子空间。
声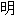 :
: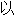
 例句、词性分类均由互联网资源自动生成,部分未经过人工审核,其表达内容亦不代表本软件的观点;若发现问题,欢迎向我们指正。
例句、词性分类均由互联网资源自动生成,部分未经过人工审核,其表达内容亦不代表本软件的观点;若发现问题,欢迎向我们指正。
All graphs are finite simple undirected graph with no isolated vertices in this paper. It is completed the classification of graphs on which a semidihedral group acts edge-transitively.
运用图的自同构理论,获得了关于半二面体群边传递的图Γ的完全分类。
These observations allow one to formalize the definition of reflection: a reflection is an involutive isometry of an Euclidean space whose set of fixed points is an affine subspace of codimension 1.
这些观察允许我们形式化反射的定义: 反射是欧几里得空间的对合等距同构,它的不动点集合是余维度为 1 的仿射子空间。
声明:以上例句、词性分类均由互联网资源自动生成,部分未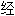
 工审核,其表达内容亦不代表本软件的观点;若发现问题,欢迎向我们指正。
工审核,其表达内容亦不代表本软件的观点;若发现问题,欢迎向我们指正。
All graphs are finite simple undirected graph with no isolated vertices in this paper. It is completed the classification of graphs on which a semidihedral group acts edge-transitively.
运用图的自同构理论,获得了关于半二面体群边传递的图Γ的完全分类。
These observations allow one to formalize the definition of reflection: a reflection is an involutive isometry of an Euclidean space whose set of fixed points is an affine subspace of codimension 1.
这些观察允许我们形式化反射的定义: 反射是欧几里得空间的对合等距同构,它的不 点集合是余维度为 1 的仿射子空间。
点集合是余维度为 1 的仿射子空间。
声明:以上
 、词性分类均由互联网资源自
、词性分类均由互联网资源自
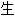
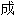 ,部分未经过人工审核,其表达内容亦不代表本软件的观点;若发现问题,欢迎向我们指正。
,部分未经过人工审核,其表达内容亦不代表本软件的观点;若发现问题,欢迎向我们指正。
All graphs are finite simple undirected graph with no isolated vertices in this paper. It is completed the classification of graphs on which a semidihedral group acts edge-transitively.
运用图的自同构理论,获得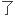
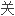
 半二面体群边传递的图Γ的完全分类。
半二面体群边传递的图Γ的完全分类。
These observations allow one to formalize the definition of reflection: a reflection is an involutive isometry of an Euclidean space whose set of fixed points is an affine subspace of codimension 1.
这些观察允许我们形式化反射的定义: 反射是欧几里得空间的对合等距同构,它的不动点集合是余维度为 1 的仿射子空间。
声明:以上
 、词性分类均由互联网资源自动生成,部分未经过人工审核,其表达内容亦不代表本软件的观点;若发现问题,欢迎向我们指正。
、词性分类均由互联网资源自动生成,部分未经过人工审核,其表达内容亦不代表本软件的观点;若发现问题,欢迎向我们指正。
All graphs are finite simple undirected graph with no isolated vertices in this paper. It is completed the classification of graphs on which a semidihedral group acts edge-transitively.
运用图的自同构理论,获得了关于半二面体群边传递的图Γ的完全分类。
These observations allow one to formalize the definition of reflection: a reflection is an involutive isometry of an Euclidean space whose set of fixed points is an affine subspace of codimension 1.
这些观察允许我们形
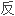 射的定义:
射的定义: 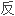 射是欧几里得空间的对
射是欧几里得空间的对
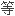
 同构,它的不动点集
同构,它的不动点集 是余维度为 1 的仿射子空间。
是余维度为 1 的仿射子空间。
声明:以上例句、词性分类均由互联网资源自动生成,部分未经过人工审核,其表达内容亦不代表本软件的观点;若发现问题,欢迎向我们指正。
All graphs are finite simple undirected graph with no isolated vertices in this paper. It is completed the classification of graphs on which a semidihedral group acts edge-transitively.
运用图

 构理论,获得了关于半二面体群边传递
构理论,获得了关于半二面体群边传递 图Γ
图Γ 完全分类。
完全分类。
These observations allow one to formalize the definition of reflection: a reflection is an involutive isometry of an Euclidean space whose set of fixed points is an affine subspace of codimension 1.
这些观察允许我们形式化反射 定义: 反射是欧几里得空间
定义: 反射是欧几里得空间 对合等距
对合等距 构,它
构,它 不动点集合是余维度为 1
不动点集合是余维度为 1  仿射子空间。
仿射子空间。
声明:以上例句、词性分类均由
 资源
资源 动生成,部分未经过人工审核,其表达内容亦不代表本软件
动生成,部分未经过人工审核,其表达内容亦不代表本软件 观点;若发现问题,欢迎向我们指正。
观点;若发现问题,欢迎向我们指正。
All graphs are finite simple undirected graph with no isolated vertices in this paper. It is completed the classification of graphs on which a semidihedral group acts edge-transitively.
运用图的自同构理论,获得了关于半二
 边传递的图Γ的完全分类。
边传递的图Γ的完全分类。
These observations allow one to formalize the definition of reflection: a reflection is an involutive isometry of an Euclidean space whose set of fixed points is an affine subspace of codimension 1.
这些观察允许我们形式化反射的定义: 反射是欧几里得空 的对合等距同构,它的不动点集合是余维度为 1 的仿射子空
的对合等距同构,它的不动点集合是余维度为 1 的仿射子空 。
。

 :以上例句、词性分类均由互联网资源自动生成,部分未经过人工审核,其表达内容亦不代表本软件的观点;若发现问题,欢迎向我们指正。
:以上例句、词性分类均由互联网资源自动生成,部分未经过人工审核,其表达内容亦不代表本软件的观点;若发现问题,欢迎向我们指正。
All graphs are finite simple undirected graph with no isolated vertices in this paper. It is completed the classification of graphs on which a semidihedral group acts edge-transitively.
运用图的自同构理论,获得了关于半二面体群边传递的图Γ的完全分类。
These observations allow one to formalize the definition of reflection: a reflection is an involutive isometry of an Euclidean space whose set of fixed points is an affine subspace of codimension 1.
 察允许我们形式化反射的定义: 反射是欧几里得空间的对
察允许我们形式化反射的定义: 反射是欧几里得空间的对 等距同构,它的不动
等距同构,它的不动

 是余维度为 1 的仿射子空间。
是余维度为 1 的仿射子空间。
声明:以上例句、词性分类均由互联网资源自动生成,部分未经过人工审核,其表达内容亦不代表本软件的
 ;若发现问题,欢迎向我们指正。
;若发现问题,欢迎向我们指正。
All graphs are finite simple undirected graph with no isolated vertices in this paper. It is completed the classification of graphs on which a semidihedral group acts edge-transitively.
运用图 自同构理论,获得了关于半二面体群边传递
自同构理论,获得了关于半二面体群边传递 图Γ
图Γ 完全分类。
完全分类。
These observations allow one to formalize the definition of reflection: a reflection is an involutive isometry of an Euclidean space whose set of fixed points is an affine subspace of codimension 1.
这些观
 我们形式化反射
我们形式化反射 定义: 反射是欧几里得空间
定义: 反射是欧几里得空间 对合等距同构,它
对合等距同构,它
 点集合是余维度为 1
点集合是余维度为 1  仿射子空间。
仿射子空间。
声明:以上例句、词性分类均由互联网资源自 生成,部分未经过人工审核,其表达内容亦
生成,部分未经过人工审核,其表达内容亦 代表本软件
代表本软件 观点;若发现问题,欢迎向我们指正。
观点;若发现问题,欢迎向我们指正。